Empirical Statistical Tests
Empirical statistical tests perform checks to determine whether a random number generator produces a random numbers that actuall behaves the way we expect random numbers to behave. One of the most well-respected statistical test suites is TestU01 (see also the TestU01 Wikipedia page).
Amazingly, most of the generators in widest use don't survive even very minimal statistical testing.
All generators in the PCG family do very well in statistical tests.
TestU01's SmallCrush Battery
This test battery applies a small number of statistical tests, each of which uses only a small number of random numbers. It runs in just a few seconds.
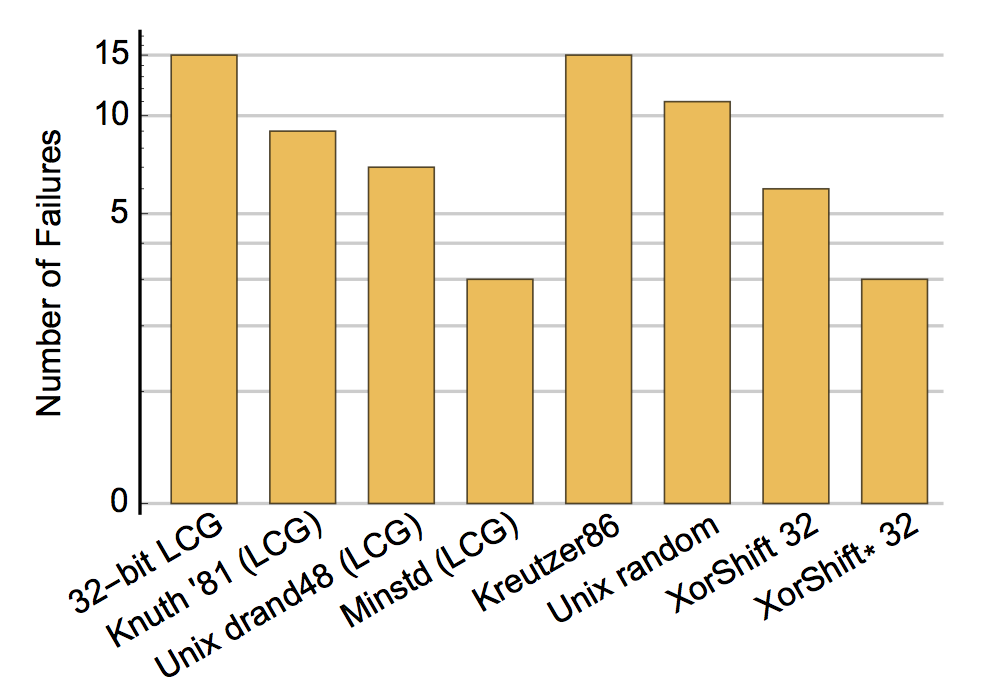
TestU01's SmallCrush battery.
The graph uses a log scale because even one failure indicates a problem. This test is quite challenging for a 32-bit generator to pass (although the PCG family has 32-bit generators that can pass this test). XorShift* is actually quite a good generation technique, but XorShift* cannot pass SmallCrush with only 32 bits of state.
TestU01's LinearComp Test
TestU01's SmallCrush battery only runs fifteen tests from its library of numerous statistical tests. One omitted test that can also be run quickly is its “linear complexity” test. This test is interesting because it can run in only a couple of seconds, and reveals problems in several widely-used RNGs that are not exposed by running the SmallCrush Battery.
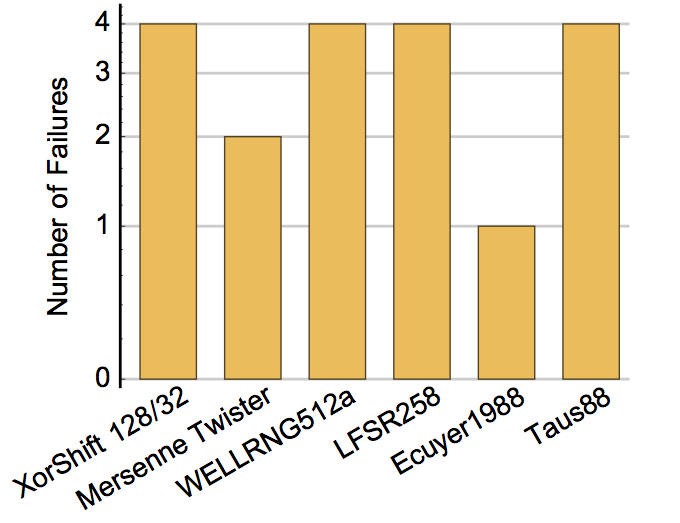
TestU01's LinearComp test (at four sizes).
Here, the LinearComp test is run at sizes 5000, 25000, 50000, and 75000. Again the graph uses a log scale because even one failure indicates a problem.
This test is interesting because it takes down every generator that is just a linear-feedback shift register generator, including generalized ones like XorShift.
TestU01's Crush and BigCrush Batteries
TestU01 provides two batteries that are much more thorough than SmallCrush.
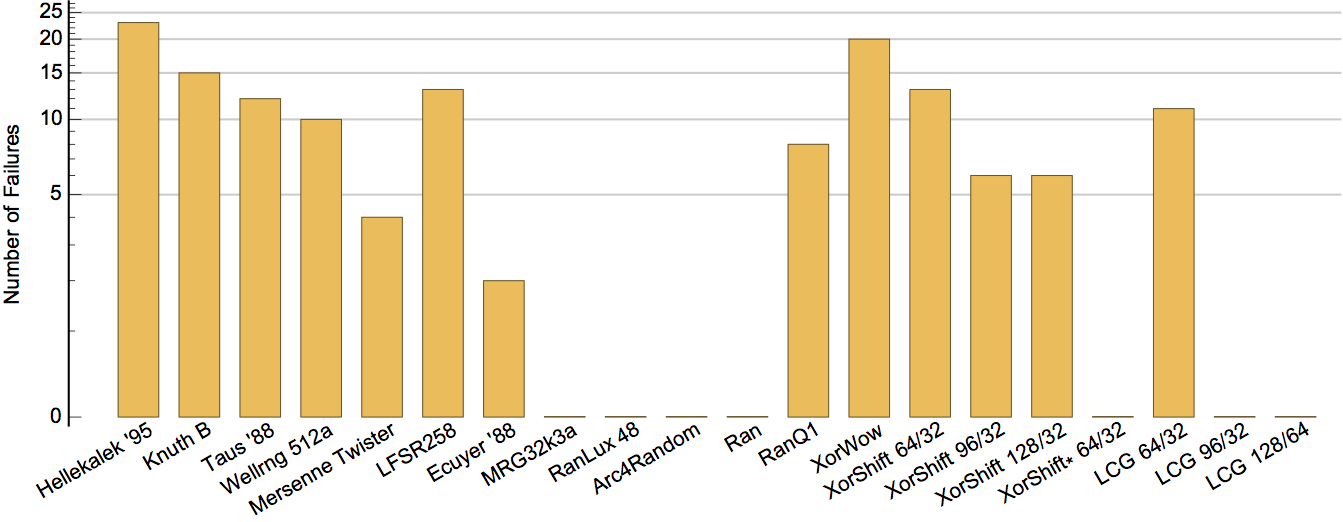
Combined results for TestU01's Crush and BigCrush batteries.
Many well known (and not so well known) RNGs cannot pass these test batteries.
Statistical Performance of the PCG Family
The PCG family does very well in statistical tests.
Almost all the RNGs provided in the PCG library pass TestU01's BigCrush test battery (as well as Crush and SmallCrush). In fact, they pass the tests with a huge margin, which means that even if someone developed a ReallyHugeCrush variant, they would pass that test, too. In fact, some members pass with the widest margin that is theoretically possible.
There is, however, one situation where we can't expect any uniform RNG (even a theoretically ideal one) to pass BigCrush or Crush. A RNG's ability to pass statistical tests depends on how much internal state it has—with less internal state, passing statistical tests becomes more difficult (imagine how hard it would be with only one bit of state!). No uniform RNG can pass Crush or BigCrush with only 32 bits of internal state (see the PCG paper for details). Even passing SmallCrush is very difficult (it's theoretically possible, but just barely). PCG library provides some very tiny generators for space-constrained applications (as well as some other scenarios), including a tiny 32-bit uniform generator that does pass SmallCrush with only 32 bits of state. Very few RNGs exist that can pass SmallCrush with so little state.
The PCG paper discusses these issues in considerable depth, describing the statistical performance of all the members of the PCG library in detail, as well as developing the background theory for the statistical performance of theoretically ideal uniform RNGs with finite state and the concept of passing with a significant margin (a.k.a. headroom).